
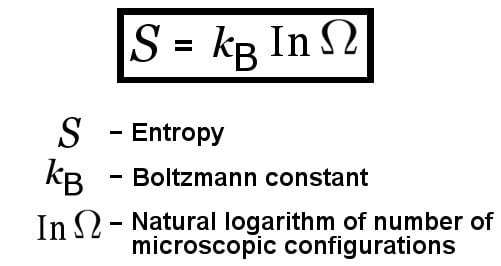
In this study, entropy change from state 0 (280 K) to state 1 (320, 375, 468, 583, and 726 K) was considered. The harmonic oscillator system and the alanine dipeptide were analyzed using the former method, whereas WHAM was applied to HP35.Ī second example is an alanine dipeptide in the gas phase, which has been studied using various techniques. The second method is a weighted histogram analysis method (WHAM). The first method is simple, where p i ( ϵ ) ( i = 0 or 1) is determined by p i ( ϵ ) = ρ M ( ϵ i ) ρ M ( ϵ 0 ) + ρ M ( ϵ 1 ). In this study, two methods were applied to obtain p 0 ( ϵ ) and p 1 ( ϵ ). However, in practical simulation time, ρ M ∗ ( ϵ 1 ) is not strictly equal to ρ M ( ϵ 1 ), especially in the region where ρ M ∗ ( ϵ 1 ) has a small value. If an infinite-time simulation could be performed, ρ M ( ϵ 1 ) and ρ M ∗ ( ϵ 1 ) would converge to the same value. ρ M ∗ ( ϵ 1 ) is a weighted energy distribution 18 18. To construct from ρ M ( ϵ 1 ) and ρ M ( ϵ 0 ) the approximated energy distribution ρ ( ϵ 1 ) that can be applied to Eq. To obtain converged values, the ranges in ϵ of ρ M ( ϵ 0 ) and ρ M ( ϵ 1 ) must be identical. If the data obtained by molecular simulation, ρ M ( ϵ 0 ) and ρ M ( ϵ 1 ), are employed, then ln usually diverges. (11), the calculation of the second term is critical. Δ Z DFT / HNC corrects Δ Z LTI with the first and second terms. Δ Z DFT / HNC with the ρ ( ϵ, 1 ) gives exact Δ Z in Eq. Exact ρ ( ϵ, 1 ) is rewritten as ρ ( ϵ 0 ) exp ( − β 0 ϵ ) ∫ d r exp / ∫ d r exp. However, Δ Z DFT / HNC gives exact expression if employed ρ ( ϵ 0 ) and ρ ( ϵ 1 ) are exact, while Δ Z LTI does not. Įquation (11) was derived with HNC approximation. (9) and (10) and the Ornstein–Zernike-type equation, 8 8. ϵ denotes total potential energy, while the same symbol represents the pair energy in the previous study (Ref. Where c ( ϵ λ ) is a direct correlation function in the energy representation. In the present approach, we use the following hypernetted-chain (HNC) approximation: 8 8. Where ζ ( ϵ λ ) is an indirect part of the energy representation. The expression for ρ ( ϵ λ ) can be formally written as ρ ( ϵ λ ) = ρ ( ϵ 0 ) exp , In this study, we use another robust approximation. Where U 1 ( r N ) = ( β 1 / β 0 ) V 1 ( r N ) and U 0 ( r N ) = V 0 ( r N ). U λ is an effective potential which connects between states 0 and 1 as follows: U λ ( r N ) = λ U 1 ( r N ) + ( 1 − λ ) U 0 ( r N ) , Δ Z is rewritten as follows: Δ Z = β 0 ∫ 0 1 d λ ∫ exp d r N ∫ exp d r N. In the following discussions, the first term of ideal gas part was omitted. Where Λ i is the de Broglie thermal wavelength and N is the number of the particles. The entropy change between states 0 and 1 is given by Δ S = S 1 − S 0 = k B = − ln ( Λ 0 Λ 1 ) 3 N + Δ Z ,


 0 kommentar(er)
0 kommentar(er)
